
들어가면서
세상에 어떤 조작을 가하여 목표를 이루고자 하는 모든 존재는, 베이즈적 사고를 해야 좋은 결정을 내릴 수 있다. (p. 14)
프로덕트 오너(Product Owner)로 일하면서 가장 고민하는 것은 '좋은 의사결정'에 대한 고민이다. 의사결정을 잘한다는 것에는 빠른 상황판단이나 유관 부서와 이해 관계자를 고려하는 등 여러 가지 요소가 포함된다.
여러 요소 중 내가 중요하게 생각하는 것은 데이터 활용도다. 이전보다 다양한 자료를 구하기 쉬워진 세상에서, 데이터를 기반으로 불확실한 상황 속 의미 있는 정보를 추출하고 판단하는 것이 훨씬 중요해졌기 때문이다. 그래서 데이터 분석가에서 직무를 변경한 요즘도 통계나 수학 관련 공부는 조금씩 하려고 노력하고 있다.

의사결정과 관련된 통계 이론 중 가장 중요하다고 생각하는 이론은 베이즈 정리다. 간단하게 말하면, 우리가 가진 정보를 바탕으로 확률을 예측하는 것이다. 오늘날의 스팸 필터, 검색, 상품 추천을 포함한 인공지능 분야의 기본 이론이면서, 의사결정을 돕는 강력한 이론이다. 하지만 기존 우리가 가진 확률에 대한 생각과 반대되기 때문에, '역확률'이라고도 불리며 이해하는 것이 쉽지는 않다.
오늘 글에서는 도서 <모든 것은 예측 가능하다>에 대한 리뷰지만, 읽으면서 최대한 쉽게 베이즈 정리와 내가 흥미를 느낀 내용에 대해서 정리해보고자 한다.
우리는 어떻게 예측하고 사고하는가
토마스 베이즈는 18세기에 활동한 영국의 목회자다. 목회자로 일했지만, 독학으로 수학과 확률론을 공부했고, 베이즈 사후에 프라이스에 의해 발표된 논문인 "An Essay Towards Solving a Problem in the Doctrine of Chances(확률론에서 문제 해결을 위한 시도)" (1763)을 통해서 발표된 것이 베이즈 정리다.
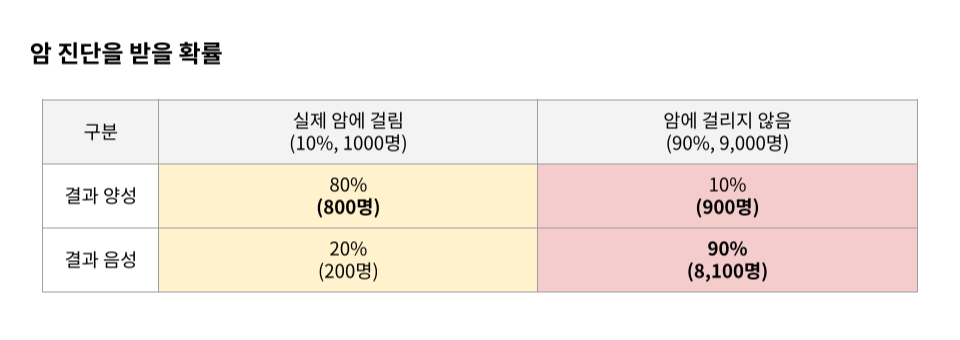
베이즈 통계와 관련해서 가장 많이 제시되는 것이 암 진단과 관련된 사례다. (통계학과 의학이 서로 보완하면서 발전해 왔기 때문에, 이런 통계 사례에는 의학 관련 사례가 많이 나온다.)

- 암에 걸린 사람의 80%의 확률로 양성으로 정확하게 잡아낸다.
- 암에 걸린 사람을 20%의 확률로 음성으로 잘못 잡아낸다.
- 암에 걸리지 않은 사람을 90%의 확률로 건강하다고 잡아낸다.
- 암에 걸리지 않은 사람을 10%의 확률로 암이 걸렸다고 오진한다.
이때 어떤 사람이 양성이라고 진단을 받았다면, 실제로 암에 걸렸을 확률은 얼마라고 예측할 수 있을까? 보통 이런 문제에 대해서 암에 걸린 사람의 80%가 정확하게 양성 판정을 받는다는 점 때문에, 80% 내외에서 확률을 생각할 수 있다.
그런데 베이즈 통계는 이런 우리의 직관과 전혀 다른 결과를 보여준다. 여기에는 사전 확률(Prior probability)이라는 것이 적용된다. 우리가 어떤 사건을 분석하기 전, 이와 관련해서 이미 알고 있거나 가정한 정보를 바탕으로 설정한 확률을 말한다.
만약 우리가 전 국민 중 암에 걸리는 사람이 1% 수준이라는 정보를 알고 있다면, 이야기가 달라질 수 있다. 아래의 표처럼 전 국민을 10,000명이라고 가정할 때, 양성 결과를 받는 사람은 1,070명(80명+990명)이 된다. 이들 중 실제 양성인 사람은 80명이기 때문에, 양성 판단을 받은 사람이 실제 양성일 확률(사후확률)은 7.4%(=80/1,070)가 된다.

하지만 사전 확률이 달라진다면, 사후 확률 또한 달라질 수 있다.
만약 예측치에 반영한 통계가 전 국민 중 1%라는 통계가 아니라, 진단받은 사람이 속한 집단 특성을 반영한다고 가정해 보자. 나이가 많고, 가족력이 있는 사람들 중 10%가 걸렸다고 가정하면 내용이 달라진다. 가족력이 있는 사람 10,000명 중 양성 결과를 받는 사람은 1,700명이 된다. 이들 중 800명이기 실제 양성이기 때문에, 실제 양성일 확률(사후확률)은 47.1%(=800/1,700)까지 올라간다.
이처럼 베이즈 통계는 '사전 확률을 어떻게 설정하는가'에 따라서 결과값이 크게 달라질 수 있다. 따라서 적절한 사전 확률을 설정해야 하며, 정보의 업데이트 등으로 사전확률을 개선할 수 있다면 더욱 유의미한 추론을 할 수 있다. 이런 이유에서 데이터가 넘치는 정보화 시대에서 검색엔진, 인공지능 등에 이런 베이즈 통계가 활용되고 있는 것이다.

이처럼 우리가 어떤 것을 예측할 때, 지나치게 생뚱맞은 예측은 하지 않는다. 우리가 과거에 수집한 정보를 나름대로의 사전 확률을 설정하고, 이를 토대로 의사결정을 하거나 예측을 하고 있다. 직관에 반하면서도, 가장 직관적으로 알고 있는 것이 이 베이즈 통계라고 말할 수 있겠다.
베이즈 통계의 철학적인 의미
이 책은 베이즈의 생애, 그리고 베이즈 통계의 철학적 의미나 역사적으로 이어져오는 논쟁을 밝히는 것에 집중하고 있다. 통계의 개념이나 응용 사례를 다루는 일반적인 통계 서적과 차이가 있다는 점에서 꽤나 흥미가 있었다.
베이즈는 확률의 패러다임을 바꿨다. 기존에는 가설이 잘못됐을 때, 이런 데이터가 나올 확률인 표집확률 방식이 주된 방식이었다. 우리가 일반적으로 귀무가설과 대립가설, 그리고 p값으로 부르는 것이 이와 연관된 개념이다. 반면 베이즈 통계는 어떤 결과가 나왔을 때, 가설이 맞을 가능성을 판단하는 방식으로 추론확률이라 부른다. 개념이 조금 어려워서 아래에서 설명을 보충해보겠다.
OTT나 쿠팡처럼 구독 모델 업체들이 구독료를 올린다는 소식이 들리면, 항상 '구독을 취소한다' 같은 댓글이 달린다. 그래서 '구독료 인상이 고객 이탈을 유발할까'에 대해 분석한다고 가정해 보자.

표집확률 방식을 활용한다면 우선 귀무가설을 세운다. 즉, '요금 인상은 고객 이탈에 영향을 미치지 않았다'는 가설을 세우는 것이다. 왜 이런 반대되는 명제인 '귀무가설을 세워서 증명하는가' 생각해 보면 통계학은 확실성을 증명하는 것이 어렵다고 판단하기 때문이다. 어떤 가설이 사실임을 증명하려면, 표본이 아닌 전체에 대해서 살펴봐야 한다.
하지만 그런 접근 방식이 현실적으로 불가능하기 때문에, 차라리 명제와 반대되는 귀무가설을 세우고, 관찰된 데이터가 이 귀무가설과 얼마나 부합하지 않는지를 보면서 우리가 세운 명제가 참에 가까움을 증명하는 것이다.
따라서 '요금 인상이 고객 이탈에 영향을 미치지 않았다'는 귀무가설에 대해서 p값이 0.01(1%)로 나온다면 관찰된 데이터에서 귀무가설을 증명할 데이터가 나올 확률이 1% 정도라는 것이다. 그래서 p값이 0.05보다 낮기 때문에, 귀무가설을 기각하게 되며 이를 토대로 '요금 인상은 고객 이탈에 영향을 미쳤다'는 것을 증명하게 된다.
반면 베이즈 통계와 같은 추론확률 방식은 지금 있는 데이터를 바탕으로 가설이 맞을지 증명하는 방식이다. 요금 인상이 고객 이탈에 영향을 미쳤을 가능성에 대해서 바로 들어간다. 우리에게는 이 방식이 맞는 것처럼 보이지만 이 방식은 앞서 표집확률 방식과는 반대이기 때문에, 우리가 추론확률을 역확률이라 부르게 된다. 위에서 정리했던 것처럼 사전확률을 세우고, 이를 토대로 사후확률을 구하게 된다. 그것이 기존 방식과의 차이라고 볼 수 있다.
추론확률을 통해 베이즈는 확률이 객관적인 것이 아닌 주관적인 영역이라고 말한다. 우리는 세상을 다 알 수 없으며, 확률은 우리가 알고 있는 사전 지식으로 내리는 것이기 때문에 세상의 속성이 아닌 이해의 속성이라고 말한다. 이는 곧, 확률이란 단순히 수학적 계산에 그치는 것이 아니라, 우리가 세상을 어떻게 받아들이고 해석하는지를 보여주는 창이라는 점을 강조한다. 베이즈 확률론은 불완전한 정보를 바탕으로 합리적인 결정을 내리는 데 필수적인 도구가 되며, 이를 통해 우리는 불확실성 속에서도 더 나은 이해와 통찰을 얻을 수 있다.
끝으로
베이즈 통계는 우리의 사고방식을 보다 유연하고 적응적으로 만들어줬다는 점에서 그 의의가 있다고 볼 수 있다. 실제 정반합의 과정으로 역사가 발전한 것처럼, 그동안 표집확률 방식에 의해서 부정을 저지르지 않고도 과학이 엉뚱한 결론을 내릴 수 있는 점을 비판하는 등 긍정적인 기여도 많았다.
하지만 사전 확률 설정이 주관적일 수 있다는 점과, '반증 가능성'으로 대표되는 칼 포퍼의 과학 철학의 비판을 받기도 했다. 그럼에도 요즘처럼 데이터가 많이 넘쳐나는 시대에서, 무시하기 어려운 개념이기 때문에 의사결정을 하는 사람이라면 베이즈 통계적 사고에 대해 관심을 가져봐도 좋을 것 같다.
Fin.
'독서기록' 카테고리의 다른 글
| '페이머스, 왜 그들만 유명할까'를 읽고 - 타인의 성공 방정식이 나에게도 적용될 수 있을까? (0) | 2025.06.22 |
|---|---|
| '데이터 드리븐 고객 경험'를 읽고 - CDP를 어떻게 구축할 것인가? (4) | 2025.06.14 |
| '나는 AI와 공부한다'를 읽고 - 우리는 모두 전문가와 관리자가 동시에 되어야한다 (2) | 2025.06.01 |
| '유니클로'를 읽고 - 현실의 연장선상에 목표를 두지 말자 (1) | 2025.05.16 |
| '이방인'을 읽고 | 세상의 상식을 맞추기 위해 살아가는 나에게 (1) | 2025.02.01 |